El recorrido del caballo de ajedrez es un problema clásico que consiste en mover un caballo por todas las casillas del tablero sin pasar dos veces por la misma casilla y siguiendo las reglas del juego. Este problema, que parece sencillo a primera vista, esconde una gran complejidad y ha sido estudiado por muchos matemáticos a lo largo de la historia. Uno de ellos fue el genial Leonhard Euler, considerado el padre de la matemática moderna, que dedicó varios trabajos a este tema en el siglo XVIII.
Euler fue el primero en realizar un análisis matemático riguroso del recorrido del caballo de ajedrez, planteando varias cuestiones y métodos para resolverlo. En su artículo Solución a una cuestión ingeniosa que parece que no ha sido analizada (Memoria de la Academia de Ciencias de Berlín, 1759), Euler describió el problema y propuso una solución para el caso de un tablero de 8x8, empezando desde una casilla cualquiera. Además, introdujo la idea de recorrido cerrado, es decir, aquel que termina en una casilla que esta a salto de caballo de la inicial, formando un ciclo. Euler demostró que existen recorridos cerrados para cualquier casilla inicial, excepto para las cuatro esquinas del tablero.
Euler también se interesó por el problema del recorrido del caballo en tableros de otros tamaños y estableció algunas condiciones para que existan recorridos cerrados. Por ejemplo, demostró que en un tablero rectangular de m x n casillas, con m y n pares, siempre hay un recorrido cerrado, salvo que m = 2 o n = 2. Según Euler, m y n deben ser pares ó m debe ser mayor o igual que 5, salvo que n sea igual a 6, en cuyo caso m puede ser 4, o bien m no puede ser 3, salvo que n sea 9 o mayor. Estas condiciones son necesarias, pero no suficientes, es decir, que si se cumplen, puede haber un recorrido cerrado, pero no se garantiza que lo haya. De hecho, Euler se equivocó al afirmar que eran suficientes, y fue corregido por el matemático estadounidense Allen Schwenk en 1991. Schwenk encontró una condición adicional que hace que las condiciones de Euler sean suficientes: Si m = 6 y n es múltiplo de 4, entonces el tablero no puede estar dividido en cuatro rectángulos de 3 x n/2 casillas cada uno, de tal forma que el caballo no pueda saltar entre ellos. Estas condiciones se pueden comprobar fácilmente con un poco de álgebra y geometría, y se basan en el hecho de que el caballo cambia el color de la casilla en cada salto, y que el número de casillas de cada color debe ser par para que haya un recorrido cerrado.
Asimismo, Euler planteó el reto de construir un cuadrado mágico al numerar los pasos sucesivos del caballo en su recorrido por el tablero, de modo que la suma de cada fila, columna y diagonal sea la misma. Euler solo pudo construir un cuadrado semimágico de orden 8, es decir, con esta propiedad para filas y columnas, pero no para diagonales. Recientemente, con ayuda de un ordenador, se demostró que no es posible construir un cuadra mágico con el recorrido del caballo.
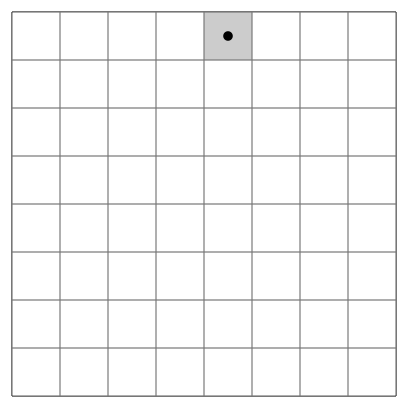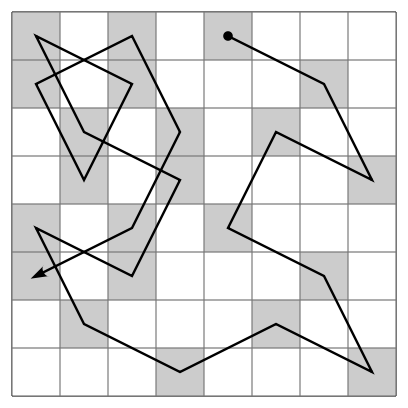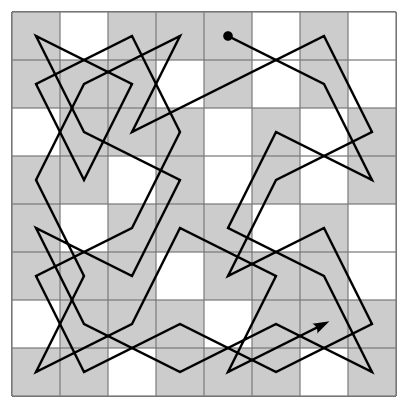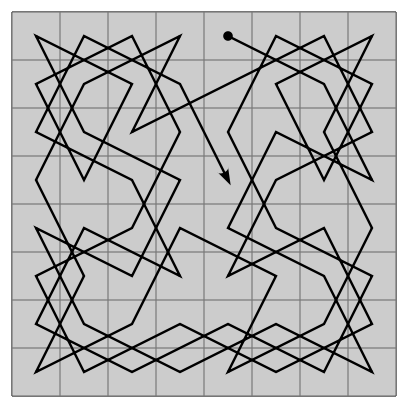
El problema del recorrido del caballo de ajedrez ha seguido atrayendo la atención de muchos matemáticos y aficionados, que han desarrollado diversas técnicas y algoritmos para resolverlo. Algunos de ellos son el método de Warnsdorff, el método de las diagonales, el método de las vueltas o el método de las espirales. Estos métodos son técnicas para encontrar un recorrido del caballo de ajedrez que pase por todas las casillas de un tablero sin repetir ninguna. Te los explico brevemente:
El método de Warnsdorff consiste en elegir siempre el movimiento que lleve al caballo a una casilla con el menor número de movimientos posibles desde ella. Así se evita dejar casillas aisladas o de difícil acceso para el final.
El método de las diagonales consiste en dividir el tablero en cuatro cuadrantes iguales y seguir un patrón de movimientos que recorra las diagonales de cada cuadrante. Por ejemplo, si el caballo empieza en la esquina superior izquierda, se mueve a la diagonal inferior derecha del primer cuadrante, luego a la diagonal superior izquierda del segundo cuadrante, y así sucesivamente.
El método de las vueltas consiste en seguir un recorrido en forma de espiral que rodee el tablero, empezando por el centro y terminando en una esquina. Se puede elegir el sentido horario o antihorario, y se debe tener en cuenta que el caballo debe saltar dos veces por cada lado del tablero, excepto por el último.
El método de las espirales consiste en seguir un recorrido en forma de espiral que atraviese el tablero, empezando por una esquina y terminando en el centro. Se puede elegir el sentido horario o antihorario, y se debe tener en cuenta que el caballo debe saltar dos veces por cada lado del tablero, excepto por el primero.
El recorrido del caballo de ajedrez es, por tanto, un ejemplo de cómo un juego puede convertirse en un desafío matemático, que estimula el ingenio, la creatividad y el razonamiento lógico. Euler fue uno de los pioneros en abordar este problema con rigor y elegancia, y sus aportaciones siguen siendo relevantes y admiradas hoy en día.
Imagen: Jakob Emanuel Handmann, Public domain, via Wikimedia Commons
Dejo aquí, un interesante vídeo acerca de este tema


.png)











No hay comentarios: